Predicción de TDAH con redes neuronales
Estudio de arquitecturas de redes neuronales recientes para datos tabulares, y compararlos en el ámbito del diagnóstico de TDAH.
Introducción
El TDAH es un trastorno del neurodesarrollo común en niños y adolescentes, caracterizado por síntomas de inatención, hiperactividad e impulsividad. La identificación temprana y precisa es crucial para el manejo efectivo del trastorno. Algunos investigadores, empezaron a utilizar el WISC-IV a fin de tratar de identificar un perfil cognitivo con el que identificar más fácilmente este trastorno. El objetivo del proyecto es evaluar el rendimiento de diversos modelos predictivos de redes neuronales recientes, en el ámbito de los datos estructurados.
Modelos Predictivos
Para el análisis comparativo, seleccioné varios modelos especializados en datos tabulares:
- TabNet: Un modelo de redes neuronales capaz de interpretar y aprender de manera efectiva relaciones no lineales en datos tabulares.
- TabTransformer: Este modelo combina la estructura de un transformer con datos tabulares, permitiendo manejar de manera eficiente tanto datos categóricos como continuos.
- Neural Oblivious Decision Ensembles (NODE): Un enfoque que integra árboles de decisión con redes neuronales, optimizando el rendimiento en datos tabulares.
- 1D-CNN: Una red neuronal convolucional de una dimensión adaptada para procesar secuencias de datos, permitiendo la detección de patrones temporales o secuenciales.
Metodología
Dataset
El dataset se compone de los resultados del test WISC-IV de varios niños, divididos en dos grupos: uno con diagnóstico de TDAH y otro grupo control. Estos resultados sirven como características de entrada para los modelos de predicción. Como características o features utilizamos los índices: Full Scale Intelligence Quotient (FSIQ), Verbal Comprehension Index (VCI), Perceptive Reasoning Index (PRI), Working Memory Index (WMI), Processing Speed Index (PSI), General Ability Index (GAI), y Cognitive Processing Index (CPI). En la figura [Figura 1] podemos observar la diferencia entre el grupo control y el grupo clínico.
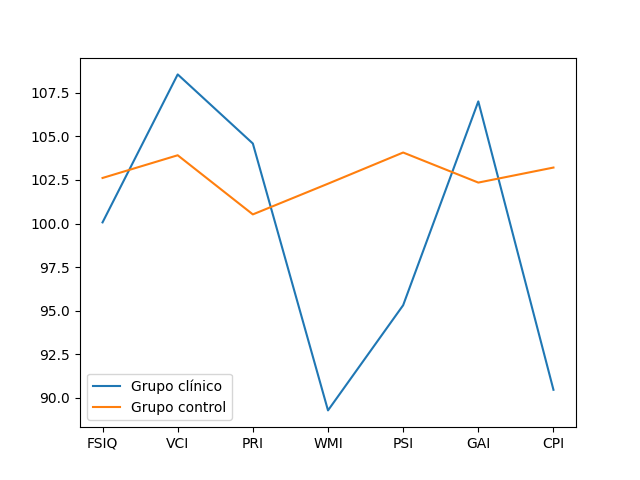Figura 1: Diferencias entre el Grupo Control y el Grupo Clínico
Preprocesado de los Datos
Como preprocesado de datos, se realizó una serie de pasos simples para evitar introducir bias en los modelos y asegurar que los datos puedan ser digeridos por los modelos:
- Eliminado de elementos duplicados
- Normalización de los valores numéricos con Standard y Robust scaling
*En este caso todas las características eran numéricas, pero si hubiesen valores de tipo categórico, habría que hacer una transformación con One-hot encoding o similar para pasar los valores categóricos a numéricos.
Evaluación de Modelos
Para evaluar el rendimiento de los modelos, utilicé una validación cruzada de 10 pliegues. Este método asegura que los resultados sean consistentes y no dependan de una sola división del dataset. El proceso consiste en dividir el conjunto de datos en 10 partes o pliegues de tamaño aproximadamente igual. Luego, se realiza un proceso iterativo en el que el modelo1 se entrena y evalúa 10 veces, cada vez utilizando un pliegue diferente como conjunto de prueba y los restantes 9 como conjunto de entrenamiento, tal y como podemos ver en la [Figura 2]. De esta manera, se obtienen 10 estimaciones del rendimiento del modelo, que se pueden promediar para obtener una medida más robusta y generalizada de su desempeño.
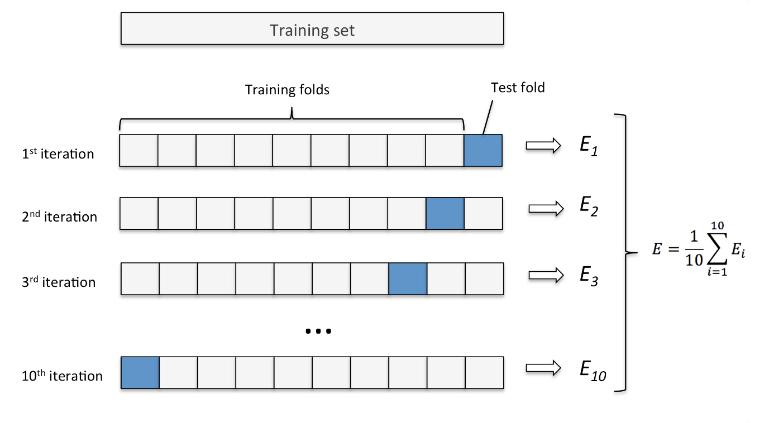Figura 2: 10 K-Fold Cross Validation
Las métricas de rendimiento utilizadas fueron el precisión, AUC-ROC, sensibilidad y especificidad:
- Precisión: La precisión es una métrica que evalúa la tasa de acierto. Se calcula dividiendo el número de aciertos entre el número de casos.
- Área bajo la curva ROC: El área bajo la curva ROC (Receiver Operating Characteristic) evalúa la capacidad discriminativa de un modelo de clasificación, y representa la tasa de verdaderos positivos (sensibilidad) en función de la tasa de falsos positivos (1 - especificidad). Cuanto mayor sea el área bajo la curva ROC, mejor será el rendimiento del modelo.
- Sensibilidad: La sensibilidad, también conocida como recall o ratio de verdaderos positivos, mide la proporción de casos positivos que son correctamente identificados por un modelo de clasificación. Es decir, evalúa la capacidad del modelo para detectar correctamente los casos positivos. Se calcula dividiendo el número de verdaderos positivos entre la suma de verdaderos positivos y falsos negativos.
- Especificidad: La especificidad mide la proporción de casos negativos que son correctamente identificados por un modelo de clasificación. Evalúa la capacidad del modelo para detectar correctamente los casos negativos. Se calcula dividiendo el número de verdaderos negativos entre la suma de verdaderos negativos y falsos positivos.
Análisis Estadístico
El análisis estadístico utilizado para evaluar qué modelos rinden mejor es el test de Wilcoxon. Este test no paramétrico se utiliza para comparar dos muestras y determinar si hay una diferencia significativa entre ellas.
En el estudio, se aplicó el test de Wilcoxon para comparar las métricas de rendimiento obtenidas, y calcular un valor de p que indica la probabilidad de observar una diferencia mayor o igual a si no hubiera diferencia real entre ellos. Es decir, se asume como hipótesis nula que no hay diferencia entre ambos rendimientos, y si el valor de p es menor que el nivel de significancia (establecido en 0.1 para un grado de confianza del 90 %), se concluye que hay una diferencia significativa entre los modelos y se puede afirmar que uno de ellos tiene un mejor desempeño que el otro.
No obstante, dado que las comparativas se realizaron entre múltiples modelos, es necesario aplicar un proceso de ajuste mediante el método de Bonferroni, el cual permite controlar la tasa global de error de tipo I. Por tanto, se calculan los p-values por pares, se realiza el ajuste de Bonferroni y se obtienen aquellos modelos que rinden mejor para el conjunto de datos.
Ajuste de Hiperparámetros
El ajuste de hiperparámetros fue realizado mediante Hyperopt, una herramienta de optimización bayesiana que permite encontrar los mejores valores para los parámetros de los modelos, maximizando su precisión.
Tecnologías utilizadas
Para el desarrollo del estudio se utilizaron:
- Python como lenguaje de programación
- Librerías de TensorFlow, PyTorch y Scikit-learn para los modelos
- Librerías de tratamiento y estructura de datos como Pandas y NumPy.
- Bibliotecas de visualización como Matplotlib y Seaborn.
Resultados
En cuanto a los resultados obtenidos durante los experimentos, por un lado, se realizó un análisis out of the box, sin ningún ajuste de parámetros, evaluando su desempeño con los valores de fábrica en dos escenarios: preprocesamiento con StandardScaler o RobustScaler. Los valores de entrenamiento utilizados para todos los modelos son: 100 épocas, early stopper con paciencia 10 pasos, 10-fold cross validation y semilla 1234.
| Modelo | Prep. | Accuracy | AUC ROC | Recall | Specificity | Tiempo |
|---|---|---|---|---|---|---|
| TabNet | Standard | 80.9 | 86.1 | 72.8 | 88.2 | 135.4s |
| TabTransformer | Standard | 83.0 | 82.7 | 76.8 | 88.5 | 295.1s |
| Node | Standard | 71.8 | 71.0 | 56.0 | 86.1 | 38.5s |
| 1DCNN | Standard | 83.9 | 83.3 | 72.0 | 94.6 | 75.6s |
| TabNet | Robust | 80.9 | 86.2 | 72.8 | 88.1 | 129s |
| TabTransformer | Robust | 85.6 | 85.4 | 81.6 | 89.3 | 263.1s |
| Node | Robust | 73.5 | 73.0 | 64.0 | 82.1 | 33s |
| 1DCNN | Robust | 83.4 | 82.7 | 71.0 | 94.2 | 70s |
Como podemos observar en la Tabla, existe una ligera diferencia entre usar StandardScaler o RobustScaler, siendo los modelos TabTransformer y Node los que obtienen mejores resultados cuando aplicamos RobustScaler, con un aumento del 3% aproximadamente, y un 8% en el caso del recall para Node. Esto nos puede indicar que los modelos mencionados son más sensibles a los outliers o valores atípicos, mientras que TabNet y el modelo convolucional 1DCNN han rendido prácticamente igual. Por tanto, en caso de tener que escoger esta configuración, el uso de RobustScaler permite mejores resultados.
Por otro lado, realizando un ajuste de hiperparámetros para maximizar el área ROC, obtenemos:
| Modelo | Prep. | Accuracy | AUC ROC | Recall | Specificity | Tiempo (s) |
|---|---|---|---|---|---|---|
| TabNet | Standard | 78.25 | 78.1 | 75.6 | 80.7 | 270.1 |
| TabTransformer | Standard | 74.9 | 75.1 | 79.2 | 71.1 | 221.4 |
| Node | Standard | 83.4 | 83.3 | 81.6 | 85.0 | 387.5 |
| 1DCNN | Standard | 84.9 | 84.4 | 74.4 | 94.3 | 424.2 |
| TabNet | Robust | 77.3 | 76.9 | 70.4 | 83.5 | 418.5 |
| TabTransformer | Robust | 80.9 | 80.7 | 77.2 | 84.2 | 214.9 |
| Node | Robust | 79.4 | 79.2 | 75.6 | 82.8 | 329.3 |
| 1DCNN | Robust | 85.1 | 84.5 | 74.8 | 94.3 | 398.9 |
Algo que llama la atención es cómo el rendimiento de los modelos con hiperparámetros en los casos de TabNet y TabTransformer es inferior a los valores por defecto. Esto, en buena medida, podría deberse a que al realizar el ajuste de HyperOpt sin utilizar k-fold, la evaluación de la función objetivo no se ajuste a la cantidad tan limitada de datos de los que disponemos, produciendo un sobreajuste de los mismos y haciendo que funcionen peor. No obstante, realizar una evaluación por k-fold de los hiperparámetros requeriría mayor coste computacional, por lo que se realizará el estudio con los mejores datos obtenidos para cada modelo,
Es notable cómo Node y 1DCNN que no utilizan mecanismos de atención en su implementación, sí consiguen una mejora sustancial en su rendimiento utilizando el ajuste de hiperparámetros.
Finalmente, se realizó un estudio comparativo, mediante el test de Wilcoxon, para determinar aquellos modelos que rinden mejor. Para poder realizar este tipo de tests estadísticos, debemos asegurar que las muestras obtenidas son pareadas o muestras independientes relacionadas. En caso contrario, deberíamos de aplicar otro tipo de tests como el análisis de varianza (ANOVA) o la prueba de Kruskal-Wallis. En nuestro caso, cada muestra corresponde al valor de AUC ROC para los distintos folds. Tenemos 4 de estas muestras, una por modelo; y dado que se han tomado bajo la misma configuración, conjunto de datos y preprocesamiento (RobustScaler), por tanto, es posible aplicar el test de Wilcoxon para realizar comparaciones emparejadas entre los modelos. Utilizamos las versiones por defecto de TabNet y TabTransformer, y aquellas con ajuste de hiperparámetros para Node y 1DNN.
Cuando se realizan múltiples comparaciones, como en el caso de comparar las métricas ROC AUC de varios modelos, existe un mayor riesgo de obtener resultados significativos de manera aleatoria debido a la inflación del error de tipo I. Por lo tanto, se necesita un ajuste de los p-values para controlar este riesgo. La fórmula del ajuste de Bonferroni es:
\[p_{ajustado} = p_{individual} / N\]donde N es el número total de comparaciones.
Al ajustar los p-valores con el método de Bonferroni, se reduce la probabilidad de obtener falsos positivos y se establece un umbral más estricto para determinar la significancia estadística en comparaciones múltiples. Esto ayuda a garantizar una interpretación más confiable y rigurosa de los resultados.
| TabNet | TabTransformer | Node | 1DCNN | |
|---|---|---|---|---|
| TabNet | - | 1.477 | 0.082 | 1.125 |
| TabTransformer | 4.705 | - | 0.006 | 1.123 |
| Node | 5.941 | 6 | - | 5.994 |
| 1DCNN | 5.033 | 4.877 | 0.012 | - |
Para leer la Tabla, debemos hacerlo de izquierda a derecha, siendo por ejemplo el primer p-value con hipótesis alternativa, los resultados de AUC ROC de TabNet son mayores que los de TabTransformer, un 1.4766.
La interpretación de los resultados vendría a ser, con un nivel de significancia del 90% (\(\alpha=0.1\)), si el valor de p ajustado, para una comparación entre dos modelos, es menor que \(\alpha\), entonces se considera que hay evidencia estadística suficiente para rechazar la hipótesis nula y concluir que hay diferencias significativas entre los modelos.
En nuestro caso, solamente tres casos cumplen que su p-valor está por debajo del nivel de significancia \(\alpha\) (0.1): el de TabNet frente a Node (p-value=0.082), el de TabTransformer frente a Node (p-value=0.006), y 1DCNN frente a Node (p-value=0.012). Por tanto, concluimos que en todos los casos, el modelo Node rinde peor que el resto de modelos, por lo que se podría descartar en un proceso de selección con un grado de confianza del 90%.
Conclusión
Este estudio demuestra el potencial de las redes neuronales avanzadas para la predicción del TDAH utilizando datos tabulares. La integración de técnicas de aprendizaje profundo con análisis estadísticos robustos y métodos de ajuste de hiperparámetros ofrece un enfoque prometedor para mejorar la precisión del diagnóstico de trastornos neuroconductuales.
¡Gracias por leer mi primer post! Espero que este proyecto sea de interés para aquellos interesados en el aprendizaje profundo, el análisis de datos y la neurociencia. Si tienen preguntas o comentarios, ¡no duden en dejarlos abajo!
Bibliografía
Costa, P.T. & Widiger, T.A. (2013). Personality Disorders and the Five-Factor Model of Personality. American Psychological Association. Disponible en: APA.
Navarro, M. (2020). Memoria de trabajo y velocidad de procesamiento evaluado mediante WISC-IV como claves en la evaluación del TDAH. Revista de Psicología Clínica con Niños y Adolescentes, 7. doi:10.21134/rpcna.2020.07.1.3.
Tocilins-Ruberts, A. (2022). Transformers for Tabular Data: TabTransformer Deep Dive. Medium. Disponible en: Medium.
Carlens, H. (2023). State of Competitive Machine Learning in 2022. ML Contests Research. Disponible en: ML Contests.
American Psychiatric Association (1994). Diagnostic criteria from DSM-IV. The Association. ISBN: 978-0-89042-064-5.
Arik, S. O. and Pfister, T. (2021). Tabnet: Attentive interpretable tabular learning. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 35, pages 6679–6687.
** Huang, X., Khetan, A., Cvitkovic, M., and Karnin, Z. (2020).** TabTransformer: Tabular data modeling using contextual embeddings. Arxiv.
Owen, S. (2021). Use hyperopt optimally with spark and MLflow to build your best model. Databricks.
Popov, S., Morozov, S., and Babenko, A. (2019). Neural oblivious decision ensembles for deep learning on tabular data. Arxiv.
Villanueva, M. (2021). Convolutional neural networks on tabular datasets (part 1). Medium.